With the recent cryptocurrency news, you’ve probably heard about encryption algorithms such as ECDSA and RSA. Both are asymmetric algorithms that be used to sign and encrypt data. Asymmetric here means that their operations require the use of a private and public key. Private key should only be held by one person, while the public key can be held by anyone.
Signing is basically using the algorithm’s private key on the data, generating a so-called signature. Both data and signature are then sent to the recipient, who uses the public key to validate the data. Since the private key should only be held by one person, we can thus be sure that the message has been sent by that specific person. It’s noteworthy that in a signed message, the message itself is still sent in plain form, it only has another couple bytes, which represent the signature. The signature itself should appear as a set of random bytes and changes significantly even if we change a single byte of the message (almost like hashing).
Encryption takes the message, digests it with the public key and the result is a set of bytes, which are usually encoded in base64 before being sent. The message can only be decrypted with a private key. This is convenient when there’s a central hub, which needs to receive encrypted data from multiple senders. This can be achieved rather easily, as we only need to distribute the public key.
So what’s the difference between RSA and ECDSA?
RSA is one of the first asymmetric algorithms and is widely used even today. Keys in RSA are based on two very large prime numbers, along with a modulus. The keys are typically in a 1024 and a 4096 bit range, with greater size meaning it’s harder to break the encryption, but also a slower encryption and decryption. Since the algorithm is relatively slow it’s more often used to decrypt keys for another, faster algorithm.
ECDSA algorithm stands for elliptic curve digital signature algorithm. Instead of large primes, this algorithm uses, as the name suggests, elliptic curves. The keys for this algorithms tend to be a lot smaller compared to RSA, for the same security level. The curve itself usually follows the following equation:
y3=x3+ax+b
Which looks something like this (based on the values of a and b):
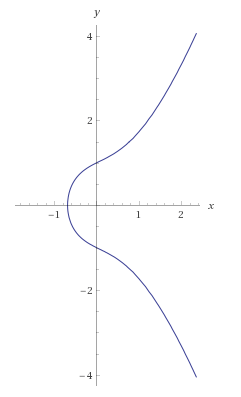
The process of encryption here is not using the simple modular exponentiation like RSA. Here we select a point on the curve and use that point to calculate a new point, based on the hash of the data we want to sign. The signature itself is another point on the curve. This may sound complicated, but given correct information, the signature creation and verification is a lot faster compared to RSA, since generating the primes needed for RSA can take a lot of time, while ECDSA only needs to generate a random number in a range. Another great thing about ECDSA is that ECDSA keys can be a lot shorter – only holding coordinates of a point on the curve, while RSA requires large primes instead. Another boon of ECDSA is that a key of 384 bits in ECDSA is equivalent to a 7680 bit key in RSA, yes you read that right, the key is shorter by a factor of 20!
While RSA is still useful for direct encryption, ECDSA is gaining traction, especially in the cryptocurrency world. ECDSA has several named curves (preset values encryption), which are used in a wide range of cryptographic applications ranging from Bitcoin (secp256k1) to FIDO (usually secp256r1). In fact, SSH utility started defaulting to ECDSA keys in version 5.7 and several certificates use ECDSA instead of RSA.
Given all this information, you may think of RSA as a rusty tool compared to ECDSA. This assumption, however, should not convince you to swap out RSA for ECDSA, as it still hasn’t been broken and still provides a (very) safe and fairly easy way to encrypt data and exchange it with others.